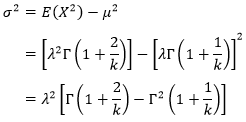Distribusi Weibull biasanya digunakan untuk menyelesaikan masalah-masalah yang menyangkut lama waktu (umur) suatu objek yang mampu bertahan hingga akhirnya objek tersebut tidak berfungsi sebagaimana mestinya (rusak atau mati).
Distribusi Weibull memiliki parameter λ dan k, dimana parameter λ dan k tersebut lebih besar dari 0.
Fungsi distribusi kumulatif dari distribusi Weibull adalah

dimana λ > 0 adalah parameter bentuk dan k > 0 adalah parameter skala. Fungsi kepadatan peluangnya adalah turunan dari fungsi distribusi kumulatifnya tersebut.

dengan demikian dapat didefinisikan fungsi kepadatan peluangnya adalah

Mean dan varian distribusi Weibull adalah
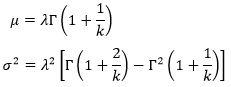
Mean dan varian dari distribusi Weibull dapat diperoleh dengan metode momen. Proses metode momen untuk mendapatkan mean dan varian adalah sebagai berikut.
Mean diperoleh dari momen pertama E(X) = µ.

pada persamaan tersebut di misalkan

maka persamaan tersebut akan menjadi

Selanjutnya disubstitusikan dengan fungsi Gamma (baca kembali Fungsi Gamma), dimana pada fungsi Gamma

dengan demikian mean distribusi Weibull adalah

Varian diperoleh persamaan

untuk menyelesaikan persamaan tersebut harus diketahui terlebih dahulu momen kedua E(X2).

hampir sama dengan penyelesaian pada momen pertama, pada persamaan di atas juga dimisalkan

Sehingga persamaannya menjadi

Selanjutnya, dapat diketahui varian dari distribusi Waibull adalah
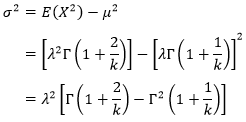
Distribusi Weibull memiliki parameter λ dan k, dimana parameter λ dan k tersebut lebih besar dari 0.
Fungsi Kepadatan Peluang
Fungsi distribusi kumulatif dari distribusi Weibull adalah

dimana λ > 0 adalah parameter bentuk dan k > 0 adalah parameter skala. Fungsi kepadatan peluangnya adalah turunan dari fungsi distribusi kumulatifnya tersebut.

dengan demikian dapat didefinisikan fungsi kepadatan peluangnya adalah

Mean dan varian distribusi Weibull adalah
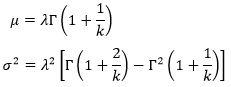
Mean dan Varian
Mean dan varian dari distribusi Weibull dapat diperoleh dengan metode momen. Proses metode momen untuk mendapatkan mean dan varian adalah sebagai berikut.
Mean
Mean diperoleh dari momen pertama E(X) = µ.

pada persamaan tersebut di misalkan

maka persamaan tersebut akan menjadi

Selanjutnya disubstitusikan dengan fungsi Gamma (baca kembali Fungsi Gamma), dimana pada fungsi Gamma

dengan demikian mean distribusi Weibull adalah

Varian
Varian diperoleh persamaan

untuk menyelesaikan persamaan tersebut harus diketahui terlebih dahulu momen kedua E(X2).

hampir sama dengan penyelesaian pada momen pertama, pada persamaan di atas juga dimisalkan

Sehingga persamaannya menjadi

Selanjutnya, dapat diketahui varian dari distribusi Waibull adalah