Rank matriks adalah jumlah maksimum dari vektor baris atau vektor kolom yang linier independen. Rank matriks ditentukan dari dimensi bujur sangkar dimana vektor baris atau kolomnya tidak bernilai nol. Jika determinan matriks bujur sangkar tidak sama dengan 0 maka rank-nya adalah ordo dari matriks bujur sangkar tersebut.
Rank matriks digunakan untuk menentukan apakah suatu matriks singular atau non-singular. Singular artinya tidak dapat di-invers-kan. Jika determinan matriks adalah 0, maka invers dari matriks tersebut tidak ada, sebab invers matriks berbanding terbalik dengan determinan. Jika determinan 0, maka akan terdapat persamaan 1/0 dalam invers matriks tersebut sehingga invers matriks tidak terdefinisikan.
Misalkan matriks A adalah matriks bujur sangkar berukuran n×n, maka matriks A dikatakan matriks singular apabila rank matriks A kecil dari n (rank(A) < n). Matriks A dikatakan matriks non-singular apabila rank matriks A sama dengan n (rank(A) = n).
Sebelum memahami lebih lanjut mengenai rank matriks, berikut diberikan penjelasan terlebih dahulu mengenai vektor baris, vektor kolom, linier independen (bebas linier) dan linier dependen (tergantung linier).
Misalkan matriks A berukuran n×p.

Vektor-vektor baris dari matriks A adalah b1, b2, … , bn, dimana

Sedangkan vektor-vektor kolom dari matriks A adalah k1, k2, … , kn, dimana

Vektor-vektor pada sebuah matriks disebut linier dependen apabila salah satu dari vektor-vektor tersebut merupakan kombinasi linier dari vektor lainnya. Sedangkan disebut linier independen apabila tidak terdapat satu pun kombinasi linier antara vektor baris yang satu dengan vektor baris yang lain.
Secara matematis, linier dependen dan linier independen dapat dipahami sebagai berikut. Misalkan vektor-vektor pada matriks A dapat dibuat menjadi suatu persamaan


Jawab:
Untuk menentukan rank dari matriks B dengan metode minor matriks, tentukan terlebih dahulu determinan dari matriks B yang berukuran 3×3.
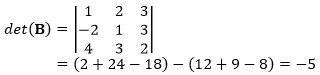













Rank matriks digunakan untuk menentukan apakah suatu matriks singular atau non-singular. Singular artinya tidak dapat di-invers-kan. Jika determinan matriks adalah 0, maka invers dari matriks tersebut tidak ada, sebab invers matriks berbanding terbalik dengan determinan. Jika determinan 0, maka akan terdapat persamaan 1/0 dalam invers matriks tersebut sehingga invers matriks tidak terdefinisikan.
Misalkan matriks A adalah matriks bujur sangkar berukuran n×n, maka matriks A dikatakan matriks singular apabila rank matriks A kecil dari n (rank(A) < n). Matriks A dikatakan matriks non-singular apabila rank matriks A sama dengan n (rank(A) = n).
Sebelum memahami lebih lanjut mengenai rank matriks, berikut diberikan penjelasan terlebih dahulu mengenai vektor baris, vektor kolom, linier independen (bebas linier) dan linier dependen (tergantung linier).
Misalkan matriks A berukuran n×p.

Vektor-vektor baris dari matriks A adalah b1, b2, … , bn, dimana

Sedangkan vektor-vektor kolom dari matriks A adalah k1, k2, … , kn, dimana

Vektor-vektor pada sebuah matriks disebut linier dependen apabila salah satu dari vektor-vektor tersebut merupakan kombinasi linier dari vektor lainnya. Sedangkan disebut linier independen apabila tidak terdapat satu pun kombinasi linier antara vektor baris yang satu dengan vektor baris yang lain.
Secara matematis, linier dependen dan linier independen dapat dipahami sebagai berikut. Misalkan vektor-vektor pada matriks A dapat dibuat menjadi suatu persamaan

dimana c1, c2, … , cp merupakan nilai konstan. Vektor-vektor k1, k2, … , kp dikatakan linier dependen apabila pada nilai konstan c1, c2, … , cp ada atau dapat diperoleh dan nilai-nilai tersebut semuanya tidak bernilai 0. Selanjutnya, vektor-vektor k1, k2, … , kp dikatakan linier independen apabila pada persamaan tersebut, nilai konstan c1, c2, … , cp tidak ada atau tidak dapat diperoleh.
Rank sebuah matriks dapat diketahui dengan metode minor matriks dan metode eliminasi gauss (metode transformasi elementer).
Metode Minor Matriks
Metode minor matriks adalah metode untuk mendapatkan rank matriks dengan menggunakan determinan minor matriks. Jika determinan minor-minor matriks yang berukuran m×m adalah nol dan determinan minor-minor matriks di bawahnya yang berukuran (m-1)×(m-1) tidak sama dengan 0, maka rank dari matriks tersebut adalah m-1.
Contoh 1
Tentukan rank dari matriks B di bawah ini dengan menggunakan metode minor matriks.
Metode Minor Matriks
Metode minor matriks adalah metode untuk mendapatkan rank matriks dengan menggunakan determinan minor matriks. Jika determinan minor-minor matriks yang berukuran m×m adalah nol dan determinan minor-minor matriks di bawahnya yang berukuran (m-1)×(m-1) tidak sama dengan 0, maka rank dari matriks tersebut adalah m-1.
Contoh 1
Tentukan rank dari matriks B di bawah ini dengan menggunakan metode minor matriks.

Jawab:
Untuk menentukan rank dari matriks B dengan metode minor matriks, tentukan terlebih dahulu determinan dari matriks B yang berukuran 3×3.
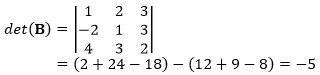
Determinan matriks B adalah -5. Nilai determinan tersebut tidak sama dengan 0, dengan demikian rank matriks B adalah 3 (rank(B) = 3).
Contoh 2
Tentukan rank dari matriks C di bawah ini dengan menggunakan metode minor matriks.
Contoh 2
Tentukan rank dari matriks C di bawah ini dengan menggunakan metode minor matriks.

Jawab:
Untuk mendapatkan mendapatkan rank matriks C, maka dicari terlebih dahulu determinan matriks C yang berukuran 3×3.

Determinan matriks C adalah 0. Dalam metode minor matriks, apabila semua determinan minor-minor matriks masih bernilai 0, maka dicari lagi determinan minor-minor di bawahnya hingga diperoleh nilai determinan minor matriknya tidak sama dengan 0.
Karena determinan matriks C adalah 0, maka dapat diketahui rank matriks C tidak sama dengan 3 (rank(C) ≠ 3), artinya rank matriks C tersebut lebih kecil dari 3 (rank(C) < 3).
Langkah selanjutnya adalah mendapatkan determinan dari minor-minor matriks C yang berukuran 2×2.

Dengan terdapatnya nilai determinan minor matriks C yang bernilai ≠ 0 telah menujukkan bahwa rank dari matriks C adalah 2 (rank(C) = 2).
Contoh 3
Tentukan rank dari matriks D di bawah ini dengan menggunakan metode minor matriks.

Jawab:
Determinan minor-minor matriks D adalah

Karena determinan dari minor-minor matriks bujur sangkarnya yang berordo 2 tidak bernilai 0 maka rank dari matriks D adalah 2 (rank(D) = 2).
Metode Eliminasi Gauss (Transformasi Elementer)
Metode eliminasi gauss disebut juga dengan metode transformasi elementer. Pada metode ini diusahakan elemen-elemen baris atau kolom dalam matriks diubah menjadi vektor 0. Maksudnya adalah agar diketahui apakah vektor tersebut linier independen atau linier dependen. Sebagaimana diketahui sebelumnya bahwa vektor 0 merupakan linier dependen.
Langkah pertama yang dilakukan dalam metode transformasi elementer adalah menentukan elemen pivot. Selanjutnya mengubah semua elemen yang sebaris menjadi 0 dengan memanfaatkan pivot yang telah ditentukan tersebut. Langkah-langkah tersebut dilakukan sampai semua baris sehingga di dalam matrik tersebut membentuk matriks identitas.

atau

Sebagai ilustrasi, diberikan beberapa buah contoh sebagai berikut.
Contoh 1
Tentukan rank dari matriks B di bawah ini dengan menggunakan metode eliminasi gauss.

Jawab:

Dari hasil transformasi diperoleh matriks identitas berukuran 3×3, sehingga rank dari matriks B adalah 3 (rank(B) = 3).
Contoh 2
Tentukan rank dari matriks C di bawah ini dengan menggunakan metode eliminasi gauss.

Jawab:

Dari hasil transformasi elementer diperoleh nilai matriks identitas berukuran 2×2, dengan demikian rank dari matriks C adalah 2 (rank(C) = 2).
Contoh 3
Tentukan rank dari matriks D di bawah ini dengan menggunakan metode eliminasi gauss.

Jawab:

Hasil transformasi elementer menunjukkan bahwa matriks identitas yang terbentuk berukuran 2×2, dengan demikian rank dari matriks D adalah 2 (rank(D) = 2).